Postulates - Assumptions
Euclid’s postulates are a set of assumptions that describe geometry. These postulates are the smallest necessary set of assumptions required for Euclid’s proofs.
Postulates (Assumptions):
- To draw a straight line from any point to any point
- A finite straight line is a line between any two points
- To produce a finite straight line continuous in a straight line
- A finite continuous straight line exists
- To Describe a circle with any center and distance
- A circle can exist with any radius
- That, if a straight lines falling on two straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side which are the angles less than the two right angles
- Two skewed lines will intersect on the side where the angle is acute.
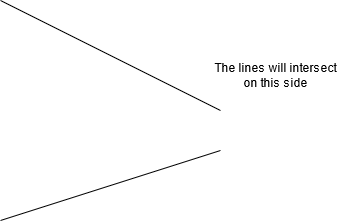
- Two skewed lines will intersect on the side where the angle is acute.
Notions - Axioms
Notions are axioms for Euclid’s Elements. These axioms do not match modern geometry. Modern axioms encompass all assumptions made by Euclid in a different form. Allowing for all Euclid’s proofs to remain valid while expanding their scope. Some interpretations of Euclid cite more notions. Only the following four are the necessary set.
Axioms provide the boundaries of the universe in which any theorems are true. Euclid proved several properties of lines and angles within these boundaries. When boundaries change, the truth of the theorem does as well. In modern math, we separate geometry into the Euclidian and non-Euclidian spaces. Euclid’s theorems are all truth on a flat 2D plane. Changing the boundaries allows the plane to bend in three dimensions. Drawing parallel lines on a bending plane may lead to an intersection. Violating many core theorems of Euclidean geometry. Anything that changes the boundary conditions may change the truth of the statement.
Notions (Axioms):
- Things which are equal to the same thing are also equal to one another
- Transitive property applies to geometry. If two triangles are equal to the same triangle, then they are equal. If A = B and B = C, then A = C
- If equals be added to equals, the wholes are equal
- Euclid’s statement applies to geometry. That is two lines create a line and two rectangles added will create a rectangle.
- If equals be subtracted from equals, the remainders are equal
- Subtracting a rectangle from a rectangle leaves a rectangle. Subtracting an angle from an angle leaves an angle.
- Things which coincide with one another are equal to one another
- Two angles of equal pairs of lines are equal.
- The whole is greater than the part
- If A + B = C, then C > A and C > B. Again, consider the application is geometry so both A and B are non-zero or existent geometry.
Sources
Euclid, Euclid’s Elements. Santa Fe, NM: Green Lion Press, 2002.